Articles
- Page Path
- HOME > J Korean Acad Nurs > Volume 51(6); 2021 > Article
- Editorial Practical Consideration of Factor Analysis for the Assessment of Construct Validity
- Jin-Hee Park, Jeung-Im Kim
-
Journal of Korean Academy of Nursing 2021;51(6):643-647.
DOI: https://doi.org/10.4040/jkan.51601
Published online: December 31, 2021

2School of Nursing, Soonchunhyang University, Cheonan, Korea

Published online Dec 31, 2021.
https://doi.org/10.4040/jkan.51601
Practical Consideration of Factor Analysis for the Assessment of Construct Validity
INTRODUCTION
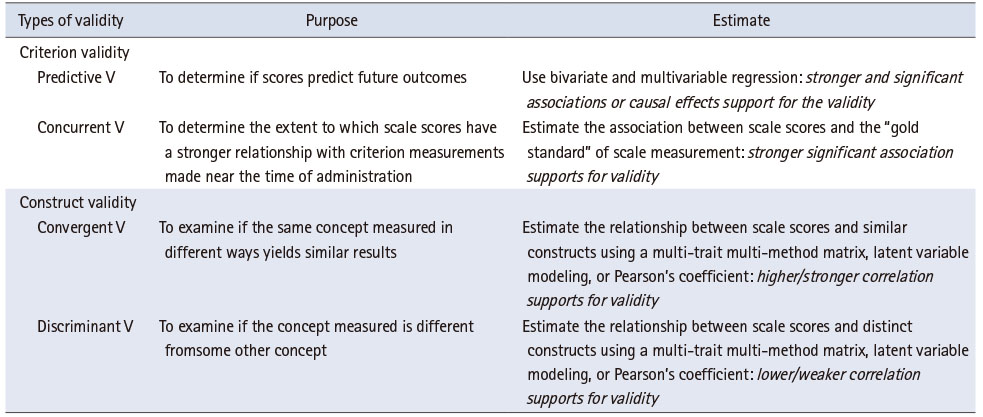
Measurement is an essential component of scientific research, whether in natural, social, or health sciences. However, there is little discussion regarding issues of measurement, especially among nursing researchers. Measurement plays an essential role in research in the health sciences field along with other scientific disciplines. Like other natural sciences, measurement is a fundamental part of the discipline and has been approached through the development of appropriate instrumentation [1]. In the field of nursing research, it is necessary to strictly verify the validity and reliability of measurements, and consider their practical importance. Researchers have been able to prepare reports after performing studies to develop the scales of measurement [2]. Three guidelines are followed: the Standards for Educational and Psychological Testing [3], the Standards for Reporting of Diagnostic Accuracy (STARD) initiative [4], and the Guidelines for Reporting Reliability and Agreement Studies [5]. Many leading biomedical journals that publish reports of diagnostic tests, such as the Annals of Internal Medicine, The Journal of the American Medical Association, Radiology, The Lancet, the British Medical Association, and Clinical Chemistry and Laboratory Medicine, have adopted STARD, along with journals in psychology such as the Journal of Personality Assessment [2]. The standards of reliability and validity can be seen in Table 1.
Table 1
Reporting Reliability and Validity
Development and validation of a scale is a time-consuming job. After the scale has been qualitatively developed, it goes through a rigorous process of quantitative examination and its score reliability and validation are measured. This includes measurement of construct, concurrent, predictive, concurrent, and discriminant validity. There are numerous techniques to evaluate construct validity such as using exploratory factor analysis (EFA), confirmatory factor analysis (CFA), or using a structural equation model. In this editorial, we will discuss the major issues in using factor analysis, a widely used method for validating scales. EFA and CFA differ greatly in assumptions, approaches, and applications, and should therefore be understood correctly and applied appropriately.
FACTORS TO BE CONSIDERED IN EXPLORATORY FACTOR ANALYSIS
EFA is used to reduce the number of measured variables to investigate the structure between the variables, and the increasing statistical efficiency. It is used when the relationship between observed variables and factors has not been theoretically established or logically organized. All observed variables are assumed to be influenced by all factors (each factor is related to all observed variables), based on which an observed variable highly correlated with a factor (and with low correlation with other factors) is extracted to reduce the number of variables. Consequently, EFA is data-driven as it accepts the results as is, rather than based on the theoretical background or literature review [6].
To check the suitability of the data for factor analysis, the Kaiser–Meyer–Olkin and Bartlett’s test of sphericity is performed beforehand. Factor analysis is performed in three steps: factor extraction, rotation, and cleaning. Determining the number of factors is critical as data interpretation is dependent on it. However, the most widely used “Kaiser rule” (dropping all components with Eigen values under 1.0) is also the most misused. While each significant factor should have an Eigen value of ≥ 1.0, not all factors with an Eigen value of 1.0 or above are significant. Unfortunately, many research papers make the error of accepting any factor with an Eigen value of ≥ 1.0 without any further consideration [7, 8]. The limitations of Kaiser’s rule can be overcome by using parallel analysis and scree test. Comprehensive consideration of these methods reduces over- or under-extraction of factors in determining the number of factors.
When trying to reduce the number of factors using variables, it can be difficult to figure out which variables belong to which factors. Factor rotation minimizes the complexity of factor loading, which makes interpretation easy, and enables a more detailed factor analysis.
An important difference between rotation methods is that they can create factors that are correlated or uncorrelated with each other. Four orthogonal rotation methods (equamax, orthomax, quartimax, and varimax) assume the factors are uncorrelated in the analysis. In contrast, oblique rotation methods assume that the factors are correlated [9]. In nursing research, it is theoretically reasonable to assume that factors are correlated. Researchers should apply the orthogonal or oblique rotation method by examining the correlation, and report the rotation method according to the presence or absence of correlation.
Finally, the cleaning of variables, the most difficult step of EFA, is used where convergent validity or discriminant validity is impaired, that is when factors other than those of previous studies are loaded.
FACTORS TO BE CONSIDERED IN CONFIRMATORY FACTOR ANALYSIS
The factor analysis for the purpose of validity assessment is directly connected to the conceptual base of the measuring instrument. The purpose for CFA is testing whether the results of the factor analysis procedure consistent with the specified conceptual base or framework of the instrument. Hence, CFA is conducted when the conceptual base or framework of a measuring instrument clearly specifies the dimensionality of a concept or construct. Therefore, CFA assumes that a specific observed variable is necessarily affected only by a related factor (latent variable), but not by others, based on a strong theoretical background or previous research [6]. Regarding the indicators to measure specific constructs, cases where the result of theoretical studies is reliable, CFA can be used to obtain the correct model fit index. However, if there are uncertainties over the factor structure with controversies and differences in research results, EFA may be attempted first [10]. Park et al. [11] adopted CFA, instead of EFA, to discover and validate the structure of factors identified in various studies.
To perform CFA, the model fit should be good enough and variables with little explanatory power should be removed in the process. There are a number of model fit indices with different criteria. No index has provided a perfect explanation of the model fit and there is no consensus on the appropriate index in the literature. Therefore, it is recommended that a variety of indices be used to assess the model fit [7, 10]. There are small differences in the indices recommended and used by researchers. As Boateng et al. [12] introduced, Browne and Cudeck [13] recommend RMSEA ≤ .05 as indicative of close fit, .05 ≤ RMSEA ≤ .08 as indicative of fair fit, and values > .10 as indicative of poor fit between the hypothesized model and the observed data. However, Hu and Bentler [14] have suggested RMSEA ≤ .06 may indicate a good fit. Bentler and Bonnett [15] suggest that models with overall fit indices of < .90 are generally inadequate and can be improved substantially. Hu and Bentler [14] recommend TLI ≤ .95. CFI ≥ .95 is often considered an acceptable fit. The threshold for acceptable model fit is SRMR ≤ .08.
Additionally, a CFA should have construct validity, convergent validity, and discriminant validity to be accurate. Construct validity is about ensuring that observed variables, constituting the latent variables, are created with appropriate concepts and definitions, through CFA. It is established when the standardization coefficient value, with observed variables constituting the latent variable, is 0.5 or higher. Convergent validity refers to how closely the new scale is related to other variables and measures of the same construct (construct reliability ≥ .70). In general, it is determined by construct reliability and variance extracted index (AVE > .50). Discriminant validity checks for overlap or similarity between concepts constructed between two or more latent variables. It can be verified by comparing the variance extraction index of the convergent validity and the square of correlation coefficient of each factor in Table 2 [12, 16].
Table 2
Comparison of Validity
CONCLUSION
Factor analysis is one of the most common multivariate statistical analysis in measurement for validity assessment. The EFA process is used for reducing dimensions, by extracting a small number of constructs (factors or variables) from a large number of observed variables under the assumption that all observed variables are related to all the factors (theoretical background and previous studies are insufficient). On the other hand, the CFA process is used for identifying the relationships between latent variables and observed variables (pre-determined based on a strong theoretical background and previous research). Therefore, it is crucial to develop and validate tools to measure constructs in the nursing field. We hope that this editorial will provide practical momentum for conducting a more accurate and systematic factor analysis with high validity and reliability.
CONFLICTS OF INTEREST:Park JH and Kim JI have been the Editors of JKAN since 2020. Except for that, we declare no potential conflict of interest relevant to this article.
FUNDING:This work was supported by Soonchunhyang University.
AUTHOR CONTRIBUTIONS:
Conceptualization or/and Methodology: Park JH & Kim JI.
Data curation or/and Analysis: Park JH.
Funding acquisition: None.
Investigation: Park JH & Kim JI.
Project administration or/and Supervision: Kim JI.
Resources or/and Software: Park JH & Kim JI.
Validation: Park JH & Kim JI.
Visualization: Kim JI.
Writing original draft or/and Review & Editing: Park JH & Kim JI.
ACKNOWLEDGEMENTS
None.
DATA SHARING STATEMENT
Please contact the corresponding author for data availability.
References
-
Streiner DL, Norman GR, Cairney J. Introduction to health measurement scalesStreiner DL, Norman GR, Cairney JHealth Measurement Scales: A Practical Guide to Their Development and Use [Internet]. New York (NY): Oxford University Press; c2015 [cited 2021 Dec 7].Available from: https://doi.org/10.1093/med/9780199685219.003.0001 .
-
-
Streiner DL, Norman GR, Cairney J. Reporting test resultsStreiner DL, Norman GR, Cairney JHealth Measurement Scales: A Practical Guide to Their Development and Use [Internet]. New York (NY): Oxford University Press; c2015 [cited 2021 Dec 7].Available from: https://doi.org/10.1093/med/9780199685219.003.0015 .
-
-
American Psychological Association. Technical recommendations for psychological tests and diagnostic techniques. Psychological Bulletin 1954;51(2:2):1–38. [doi: 10.1037/h0053479]
-
-
Choi CH, You YY. The study on the comparative analysis of EFA and CFA. Journal of Digital Convergence 2017;15(10):103–111. [doi: 10.14400/JDC.2017.15.10.103]
-
-
Seo W, Lee S, Kim M, Kim J. Exploratory factor analysis in psychological research: Current status and suggestions for methodological improvements. Journal of Social Science 2018;29(1):177–193. [doi: 10.16881/jss.2018.01.29.1.177]
-
-
Brown JD. Choosing the right type of rotation in PCA and EFA. Shiken: JALT Testing & Evaluation SIG Newsletter 2009 Nov;13(3):20–25.
-
-
Shin HJ. Accessing construct validity with factor analysis. Korean Policy Sciences Review 2014;18(2):217–234.
-
-
Browne MW, Cudeck R. Alternative ways of assessing model fit. In: Bollen KA, Long JS, editors. Testing Structural Equation Models. Newbury Park: Sage Publications; 1993. pp. 136-162.
-
-
Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling 1999;6(1):1–55. [doi: 10.1080/10705519909540118]
-
-
Bentler PM, Bonett DG. Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin 1980;88(3):588–606. [doi: 10.1037/0033-2909.88.3.588]
-
-
Heo J. In: AMOS structural equation model that is easily followed. Seoul: Hannarae; 2013. pp. 195-199.
-
 KSNS
KSNS
 E-SUBMISSION
E-SUBMISSION


 Cite
Cite